doi: 10.56294/sctconf2024823

Categoría: STEM (Science, Technology, Engineering and Mathematics)

ORIGINAL

Free Vibration Analysis of Toroidal Shell Segments Reinforced by Graded Graphene in Elastic Medium

Análisis de vibración libre de segmentos de carcasa toroidal reforzados con grafeno graduado en medio elástico

Ahmed S. Khalaf¹ *, Hamad M. Hasan¹ *

¹Department of Mechanical Engineering, University of Anbar. Anbar, Iraq.

Cite as: Khalaf AS, Hasan HM. Free Vibration Analysis of Toroidal Shell Segments Reinforced by Graded Graphene in Elastic Medium. Salud, Ciencia y Tecnología - Serie de Conferencias. 2024; 3:823. https://doi.org/10.56294/sctconf2024823

Submitted: 21-01-2024                        Revised: 03-04-2024                         Accepted: 27-05-2024                        Published: 28-05-2024

Editor: Dr. William Castillo-González

Note: paper presented at the 3rd Annual International Conference on Information & Sciences (AICIS’23).

ABSTRACT

This paper presents an analytical solution for free-vibration analyses of functionally graded graphene platelets (GPL) reinforced composite toroidal shells in an elastic medium. Four continuous distribution patterns of GPL are investigated in this study. The elastic properties of the shell have been calculated from the Halpin-Tsai micro-mechanical relationship. The governing partial differential equations of motion are derived based on the third-order shear deformation shell theory (TSDT). The shell equations are solved by adopting the approximated solution which satisfies simply supported BCs. The influences of the graphene weight fraction, distributions of the volume fraction, the number of waves, and the geometric and foundation parameters on the natural frequency of the toroidal shell segment are studied. It was clear that the FG-X distribution pattern outperformed other types of dispersion. Additionally, the presence of an elastic foundation increases the shell’s natural frequency.

Keyword: Free Vbration; Toroidal Shell; Elastic Foundation; Graphene Platelets; Third-Order Shear Deformation Theory.

RESUMEN

Este trabajo presenta una solución analítica para el análisis de vibraciones libres de plaquetas de grafeno funcionalmente graduadas (GPL) reforzadas con conchas toroidales compuestas en un medio elástico. En este estudio se investigan cuatro patrones de distribución continua de GPL. Las propiedades elásticas del armazón se han calculado a partir de la relación micromecánica de Halpin-Tsai. Las ecuaciones diferenciales parciales de movimiento se derivan a partir de la teoría de la cáscara de deformación por cizallamiento de tercer orden (TSDT). Las ecuaciones de la cáscara se resuelven adoptando la solución aproximada que satisface las BC simplemente apoyadas. Se estudian las influencias de la fracción de peso del grafeno, las distribuciones de la fracción de volumen, el número de ondas y los parámetros geométricos y de cimentación sobre la frecuencia natural del segmento de concha toroidal. Se puso de manifiesto que el patrón de distribución FG-X superaba a otros tipos de dispersión. Además, la presencia de una cimentación elástica aumenta la frecuencia natural del armazón.

Palabras clave: Vibración Libre; Concha Toroidal; Cimentación Elástica; Plaquetas de Grafeno; Teoría de la Deformación por Cizalladura de Tercer Orden.

INTRODUCTION

The toroidal shell segments are crucial parts in the civil, aerospace, and mechanical industries. Additionally, because of their unique structural shape and application in the fields of ocean engineering, nuclear power, and pressure vessel and piping, toroidal shells are frequently utilized as joint components or accessories. So, many researchers have studied the behavior of the analysis of the toroidal shell. Stein et al. ⁽¹⁾ published one of the earliest investigations on toroidal segments for the buckling problem using homogeneous and isotropic toroidal shell segments. Bich et al.^(2,3,4) investigated the linear and nonlinear buckling of functionally graded toroidal segments subjected to external pressure based on the classical shell theory (CST). Nguyen et al.⁽⁵⁾ studied free vibration characteristics of rotating stiffened toroidal shells based on third-order shear deformation theory (TSDT) reinforced with GPL in thermal environments using Rayleigh–Ritz procedure. Shahmohammadi et al.^(6,7) presented an analytical approach for static analyses, free-vibration, and stability of three-phase carbon fibers – (epoxy nanofillers) convex/concave toroidal shells based on the first-order shear deformation theory (FSDT). Mirjavadi et al.⁽⁸⁾ studied the nonlinear frequency-amplitude relationship of porous toroidal shells which stiffened eccentrically using classical shell theory (CST). They used Jacobi elliptic functions to solve the nonlinear governing differential equations. On the basis of shear deformation theory (SDT), Ali et al.^(9,10) investigated the nonlinear free vibration behavior and dynamic stability of orthotropic functionally graded toroidal shell segments, considering the damping effect.

As illustrated by the literature review above, the using of toroidal shell segments as an engineering structure has become extremely important in recent decades. Therefore, in this research, an analytical method is used to study the free vibration behavior of composite toroidal segments reinforced with GPLs in an elastic medium. In the mathematical model, third-order shear deformation theory has been employed to derive equations of motion. To estimate the mechanical properties of the composite toroidal shells the Halpin-Tsai micromechanical relationship has been utilized. The effects of graphene weight fraction, volume fraction distributions, waves number, radius to thickness ratio, and length to radius ratio on the dimensionless natural frequency of the toroidal shell segments are discussed in this paper.

Theoretical discerption

The parameters of a toroidal shell's geometry are as follows: circumferential radius at the equator ("a"_"0" ), the longitudinal radius of curvature (R), thickness (h), and length (L), The toroidal shell segments described in two states concave (R < 0) and convex (R > 0) shells as shown in figure 1. The displacement (u,v,w) in (x,y,z) directions. K₁(N/m³) is the Winkler foundation modulus, K₂(𝑁/𝑚) is the shear foundation modulus of the Pasternak model. The rotational radius is  a=a₀ -R(1-sin(ϕ)), For an approximately shallow toroidal shell at the torus' equator, the angle ϕ is almost equal to π/2 and sin(φ) ≈ 1 so a ≈ a0 Stein et al. ⁽¹⁾ Where x=Rdϕ,y=a₀ dθ.

Figure 1. Geometric modeling of toroidal shell segments

Material Properties

Four different volume fraction distributions are considered. Pattern 1 (uniform distribution UD), pattern 2 (FG-O) pattern 3 (FG-X), and Pattern 4 (FG-V)⁽¹¹⁾

By employing the Voigt-Reuss model, and composite rules of mixture then, elastic moduli, passion’s ratio, and density of the two-phase matrix/nanocomposite toroidal shells can be evaluated in equations (3).⁽¹²⁾

Where E_gm is the effective young modulus of two-phase GPLs and matrix-reinforced composite, and (E_m, E_g),(p_m, p_g) and (v_m, v_g) are young moduli, densities and, passion’s ratios of the matrix, and GPLs respectively. l_g, t_g and w_g are the length, thickness, and, width of GPLs f_g W_g are the volume and weight fractions of GPLs f_g* is the volume fraction of UD.

Governing Equation

Based on (TSDT) the governing differential equations of motions in the current investigation are derived. The strain components at a distance of z from the mid-surface over the thickness are:⁽¹³⁾

Where (u,v,w) and (ϕx,ϕy) denote displacement components that correspond to (x,y,z) coordinates and transverse normal rotations on the plane z = 0. The stress-strain relationship for the toroidal shell reinforced with GPLs is given by equations (5):

Using Hamilton’s principle⁽¹⁴⁾ to derive the governing equations of motion as follows:

Where δ is the variation operator, t₁ and t₂ are two arbitrary time boundaries. Π which is a potential energy. T denoted kinetic energy.

Substituting equation (7) in equation (6) and applying the Hamilton principle, the equation of motion of toroidal shell reinforced with GPLs is obtained as follows:

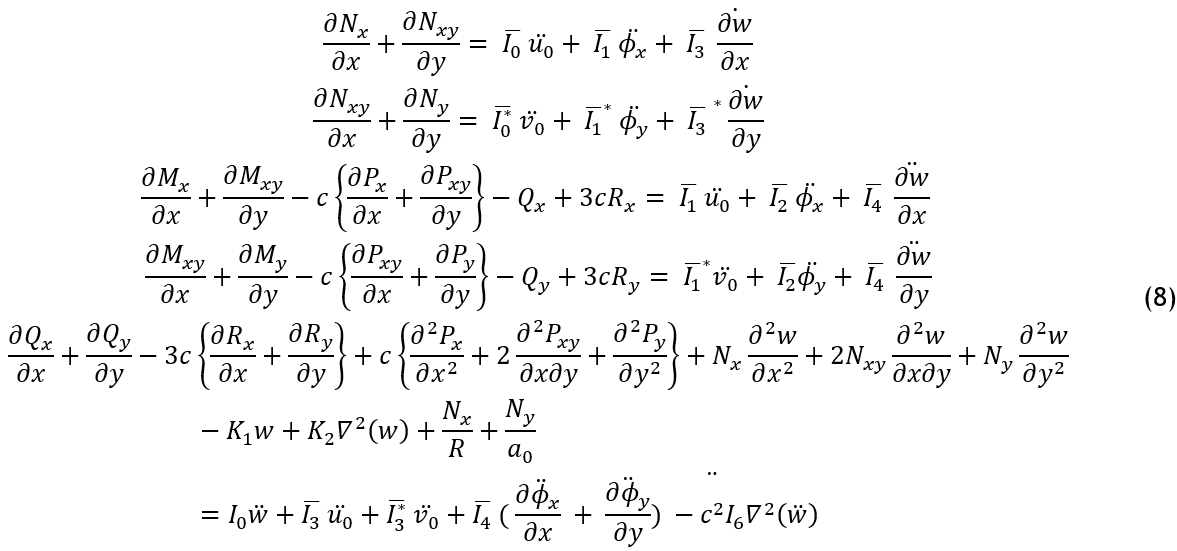
Where N_i, M_i, and Q_i are in plane forces resultant, moment resultant and, shear forces resultant respectively. While P_i and R_i are high moment and shear forces resultant. I_i represent the inertia terms, defined as follows:

Substitute equation (9) in equation (8) yields:

Where L_ij denoted to the differential operators, in the current work the Toroidal shell is assumed to be simply supported and satisfy the following boundary conditions:

The approximate solution satisfying the simply supported boundary conditions may be assumed as:⁽⁶⁾

Where U_mn, V_mn, Φ_x^mn, Φ_y^mn, and W_mn are time-independent maximum amplitudes, m, and n are a number of full and half waves in circumferential and longitudinal directions respectively. ω_mn represent the linear natural frequency of the toroidal shell. Substituting equation (13) into equation (11) yields:

Where represents the stiffness of the toroidal shell. Since the values of U_mn, V_mn, Φ_x^mn, Φ_y^mn, and W_mn are not equal to zero, then the determinant of the above 5×5 matrix must be zero. The MATLAB program is used to obtain the determinant of the matrix, calculate and, plot the linear natural frequency ω_mn.

RESULTS AND DISCUSSION

Validation

To prove the accuracy of the present solution some examples of for free vibration of cylindrical shells be provided in this Section. Be knowledgeable that when R₁→∞, a cylindrical shell can be described as a special case of a toroidal shell segment. The geometrical dimensions of the shell and foundation properties are as follows: E=2,1 Gpa,v=0,3,ρ=7850 kg/m^3,K₁=10⁷ N/m³, K₂=1,5×10⁷ N/m,h=0,001 m,L=0,41 m,a₀=0,3015 m. As a comparison to the outcomes indicated by Sofiyev et al.⁽¹⁵⁾ based on a shear deformation theory, the outcomes indicated by Shah et al.⁽¹⁶⁾ using Love first-order shell theory and a wave propagation method, and the outcomes indicated by Vuong et al.⁽¹⁷⁾ based on Third order shear deformation theory, fundamental frequencies have been calculated and listed in table 1.

Table 1. Comparisons the natural frequency of isotropic cylindrical shell ωmn/2π
n (m = 1)	Sofiyev et al.^(15)	Shah et al.^(16)	Vuong et al.^(17)	Present Study
7	5 390,6	5 324,3	5 390,59	5 324,296
8	6 085,4	6 028,8	6 085,34	6 028,754
9	6 788,8	6 739,6	6 788,75	6 739,448
10	7 498,2	7 454,6	7 498,1	7 454,41
11	8 211,9	8 172,8	8 211,78	8 172,517
12	8 329,9	8 893,5	8 928,78	8 893,07
13	9 648,6	9 616,2	9 648,42	9 615,609
14	10 370,4	10 340,6	10 370,24	10 339,817

In the present study, the influences of GPLs weight fraction, types of distribution patterns, elastic foundation, and geometric properties on the vibration of toroidal shell segments on the dimensionless frequency are investigated. mechanical properties are: E_m=2,5 GPa,E_g=1 100 GPa, ρ_m=1,15 g/cm³, ρ_g=1,06 g/cm³,v_m=0,34, v_g=0,2, l_g=2,5 μm, w_g=1,5 nm, t_g=1,06 nm.⁽⁶⁾ The shell and foundation properties used in this investigation are h = 0.01 m, a_0/h=80, R/a₀=10, L/a₀=3, W_g=1 %, m=1, n=9,K₁=K₂=0,and the dimensionless natural frequency is Ω= ω_mn a₀ √(2(ρ_m/E_m)).

The effect of waves number

The impact of the longitudinal and circumferential mode numbers on the shell's dimensionless natural frequencies (Ω) is shown in figure 2. The findings of this investigation depict the shell with uniform GPL distribution decreases in natural frequency as the circumferential mode number increase until reached the minimum value (fundamental natural frequency) of 0,2987 at m = 1 n = 9.

The impact of GPL weight fractions and distribution patterns

The influence of GPL weight fraction on the composite shell's natural frequencies is examined in figure 3 convex shell and figure 4 concave shell. Thus, when the weight fraction of the GPLs increases, the dimensionless natural frequency of the shell rises notably. The figure 3 and figure 4 also shows the effect of GPL dispersion patterns on the natural frequency where the four GPL patterns are compared to each other’s. The outcomes display in these two figures that the lowest natural frequency is associated with the FG-O dispersion and the highest natural frequency is correlated to the FG-X dispersion where the uniform and FG-V lies between FG-X and FG-O. The findings likewise show that the distribution patterns of the concave toroidal shell differ from each other more than that of the convex toroidal shell.

The FG-X pattern has a high concentration of GPLs particles on the lower and upper surfaces of the shell, making these regions stiffer and able to resist bending stresses more effectively. As a result, the FG-X distribution pattern exhibits superior performance compared to other distribution types.

Figure 2. Effect of waves numbers on the natural frequency

Figure 3. Effect of weight fraction and distribution patterns of convex shell on the natural frequency

Effect of Geometric parameters of toroidal shell

Figures 5 and 6 investigate how the geometrical parameters of the toroidal shell effect on the dimensionless natural frequencies. The FG-X dispersion pattern for the toroidal shell is utilized in this analysis, the outcomes display that whenever the L/a₀ or R/a₀increases leads to a decrease in the natural frequency, and the shell on the elastic medium has a higher natural frequency than the shell without elastic foundation. The presence of an elastic foundation increases the stiffness of the shell which increases the natural frequency.

Figure 4. Effect of weight fraction and distribution patterns of concave shell on the natural frequency

Figure 5. Effect of length to radius ratio on the natural frequency

Figure 6. Effect of radius to thickness ratio on the dimensionless natural frequency

CONCLUSIONS

The present work examines the free vibration behavior of graded GPL-reinforced composite toroidal shell segments using various distribution patterns. Simply supported boundary condition has been considered. Also, the governing differential equations were derived by employing the third-order shear deformation theory. The outcomes reached validated with three papers from the published literature. The present study provides the general conclusions listed below:

· As the weight fraction of GPL increases the dimensionless natural frequency of the toroidal shell also increases

· FG-X distribution patterns show better performance than other patterns. Where the natural frequency of FG-X is higher than other distributions.

· The differences between distribution patterns appear clearly in the concave shell, where the difference between FG-X and UD in the concave shell is quite larger than in a convex shell.

· An increase in the shell length or shell rotation radius leads to a decrease in the frequencies of the toroidal shell.

· The presence of elastic foundations leads to an increase in the frequencies of the toroidal shell.

ACKNOWLEDGMENTS

The authors would like to thank the mechanical engineering department at the University of Anbar.

REFERENCES

1. M. Stein and J. A. McElman, “Buckling of segments of toroidal shells,” AIAA J., vol. 3, no. 9, pp. 1704–1709, 1965, doi: 10.2514/3.55185.

2. B. H. Dao, N. G. Dinh, and T. I. Tran, “Buckling Analysis of Eccentrically Stiffened Functionally Graded Toroidal Shell Segments under Mechanical Load,” J. Eng. Mech., vol. 142, no. 1, pp. 1–10, 2016, doi: 10.1061/(asce)em.1943-7889.0000964.

3. D. H. Bich, D. G. Ninh, and T. I. Thinh, “Non-linear buckling analysis of FGM toroidal shell segments filled inside by an elastic medium under external pressure loads including temperature effects,” Compos. Part B Eng., vol. 87, pp. 75–91, Feb. 2016, doi: 10.1016/j.compositesb.2015.10.021.

4. D. Huy Bich, D. Van Dung, V. H. Nam, and N. Thi Phuong, “Nonlinear static and dynamic buckling analysis of imperfect eccentrically stiffened functionally graded circular cylindrical thin shells under axial compression,” Int. J. Mech. Sci., vol. 74, pp. 190–200, 2013, doi: 10.1016/j.ijmecsci.2013.06.002.

5. V. L. Nguyen, M. T. Tran, S. Limkatanyu, H. Mohammad-Sedighi, and J. Rungamornrat, “Reddy’s third-order shear deformation shell theory for free vibration analysis of rotating stiffened advanced nanocomposite toroidal shell segments in thermal environments,” Acta Mech., vol. 233, no. 11, pp. 4659–4684, 2022, doi: 10.1007/s00707-022-03347-8.

6. M. A. Shahmohammadi, S. M. Mirfatah, H. Salehipour, M. Azhari, and Ö. Civalek, “Free vibration and stability of hybrid nanocomposite-reinforced shallow toroidal shells using an extended closed-form formula based on the Galerkin method,” Mech. Adv. Mater. Struct., vol. 29, no. 26, pp. 5284–5300, 2022, doi: 10.1080/15376494.2021.1952665.

7. M. A. Shahmohammadi, S. M. Mirfatah, S. Emadi, H. Salehipour, and Ö. Civalek, “Nonlinear thermo-mechanical static analysis of toroidal shells made of nanocomposite/fiber reinforced composite plies surrounded by elastic medium,” Thin-Walled Struct., vol. 170, Jan. 2022, doi: 10.1016/j.tws.2021.108616.

8. S. S. Mirjavadi, I. Khan, M. Forsat, M. R. Barati, and A. M. S. Hamouda, “Analyzing nonlinear vibration of metal foam stiffened toroidal convex/concave shell segments considering porosity distribution,” Mech. Based Des. Struct. Mach., vol. 51, no. 1, pp. 310–326, 2023, doi: 10.1080/15397734.2020.1841654.

9. Y. Ali and H. M. Hasan, “Non-linear large amplitude vibration of orthotropic FGM convex and concave toroidal shell segments including the damping effect using the shear deformation theory,” Thin-Walled Struct., vol. 173, Apr. 2022, doi: 10.1016/j.tws.2022.109035.

10. Y. Ali and H. M. Hasan, “Nonlinear dynamic stability of an imperfect shear deformable orthotropic functionally graded material toroidal shell segments under the longitudinal constant velocity,” Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci., vol. 233, no. 19–20, pp. 6827–6850, 2019, doi: 10.1177/0954406219867991.

11. X. Li, X. C. Chen, and W. T. Jiang, “Dynamic stability of graded graphene reinforced truncated conical shells under both periodic spinning speeds and axial loads considering thermal effects,” Eng. Struct., vol. 256, Apr. 2022, doi: 10.1016/j.engstruct.2022.113963.

12. D. G. Ninh, H. Eslami, and V. N. Viet Hoang, “Dynamical behaviors of conveying-fluid nanocomposite toroidal shell segments with piezoelectric layer in thermal environment using the Reddy’s third-order shear deformation shell theory,” Thin-Walled Struct., vol. 159, Feb. 2021, doi: 10.1016/j.tws.2020.107204.

13. J. N. and C. F. L. Reddy, “a Higher-Order Shear Deformation Theory,” J. Eng. Sci., vol. 23, no. 3, pp. 319–330, 1985.

14. J. N. Reddy, Energy Principles and Variational Methods in Applied Mechanics. Wiley, 2002

15. H. Sofiyev, Z. Karaca, and Z. Zerin, “Non-linear vibration of composite orthotropic cylindrical shells on the non-linear elastic foundations within the shear deformation theory,” Compos. Struct., vol. 159, pp. 53–62, 2017, doi: 10.1016/j.compstruct.2016.09.048.

16. G. Shah, T. Mahmood, M. N. Naeem, Z. Iqbal, and S. H. Arshad, “Vibrations of functionally graded cylindrical shells based on elastic foundations,” Acta Mech., vol. 211, no. 3–4, pp. 293–307, 2010, doi: 10.1007/s00707-009-0225-9.

17. P. M. Vuong and N. D. Duc, “Nonlinear static and dynamic stability of functionally graded toroidal shell segments under axial compression,” Thin-Walled Struct., vol. 155, Oct. 2020, doi: 10.1016/j.tws.2020.106973.

FINANCING

"The authors did not receive financing for the development of this research".

CONFLICT OF INTEREST

"The authors declare that there is no conflict of interest".

AUTHORSHIP CONTRIBUTION

Conceptualization: Ahmed S. Khalaf, Hamad M. Hasan.

Data curation: Ahmed S. Khalaf, Hamad M. Hasan.

Formal analysis: Ahmed S. Khalaf, Hamad M. Hasan.

Research: Ahmed S. Khalaf, Hamad M. Hasan.

Methodology: Ahmed S. Khalaf, Hamad M. Hasan.

Drafting - original draft: Ahmed S. Khalaf, Hamad M. Hasan.

Writing - proofreading and editing: Ahmed S. Khalaf, Hamad M. Hasan.